Amateur Radio (G3TXQ) - Antenna impedance measurement
When experimenting on an antenna it's often important to determine its feedpoint impedance at various frequencies across the operating band. It's easy enough to measure SWR, but sometimes we need to know more detail than this - in particular the complex impedance at its feedpoint. Fortunately there are now several modestly priced antenna analysers on the market - such as the Palstar ZM30 and the MFJ259B - which will perform this type of meaurement with sufficient accuracy for the Radio Amateur.
Feedpoint impedance is affected by an antenna's proximity to ground, so to get meaningful results we usually want to make measurements with the antenna at a reasonable height. Unless you have very long arms or a very long step-ladder (not recommended) this means connecting the analyser to the antenna through a length of transmission line. We now have a problem: other than in very special cases, the impedance we measure with the analyser will not be the antenna's feedpoint impedance. The effect of this "transmission line transformation" can be extreme. For example, a feedpoint impedance of 25 Ohms could measure 100 Ohms on an analsyer connected to the antenna through a quarter-wavelength of 50 Ohm coaxial cable.
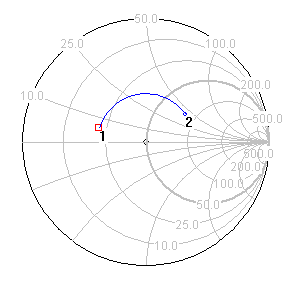
The transformation process is best visualised by reference to a Smith Chart - an example is shown on the right. Here an 80m antenna's feedpoint impedance, represented by point 1, is [22 + j6] Ohms. Introducing a length of transmission line is equivalent to rotating this point clockwise around the centre of the chart - the longer the transmission line the further the point is rotated around the chart - and line losses will move Point 2 closer to the centre of the chart. In the example shown, a 10m length of line has transformed Point 1 [22 + j6] into Point 2 [82 + j45]. In passing, note that a half-wavelength of line will rotate a point through 360° and (ignoring any cable losses) leave the impedance unchanged.
So the challenge is, given the measurement made at Point 2, to work out the antenna impedance at Point 1. In the Good (or were they bad?) Old Days we would have tackled the problem graphically with the Smith Chart, or delved into some pretty complex mathematics; fortunately, things today are a lot easier. There are numerous RF analysis programmes which will do the job for us, including some that are available on-line. One that I use regularly is the Transmission Line Calculator applet, written by W9CF. To use these tools we need to know:
- The characteristic impedance of the line
- The velocity factor of the line
- The physical length of the line
- The loss characteristics of the line
If the cable type is known, its characteristic impedance, velocity factor and loss characteristics can be found in manufacturers' tables. The physical length can of course be measured, but this must be done accurately and it's often difficult to decide exactly which two points represent the ends of the line. I prefer to make an approximate length measurement, and then calibrate the line using a known load; calibration also removes any uncertainty about the velocity factor. Here's how it works:
The feedline between my 10m monoband HexBeam test antenna and my Palstar ZM30 analyser is about 26ft of RG174 coax. Before making measurements on the antenna I placed a 22 Ohm resistor across the antenna end of the coax and measured the impedance at the other end of the coax with the ZM30 at 28.5MHz - be sure to do this at a frequency close to your antenna measurement frequency and use a load that produces an intermediate value of SWR (say 2-3) - the result was [54 + j34] Ohms. I then removed the resistor from the coax and placed it directly across the ZM30 terminals - it measured [22 + j6] Ohms.
The next step is to use these numbers to ascertain the exact electrical length of the line using the Transmission Line Calculator applet. This applet already has built-in the characteristics of some common coax cable types - unfortunately RG174 is not one of them. So I chose the "User Defined 1" cable option to input RG174 characteristics as follows:
- Ro = 50.0 (from manufacturers' data)
- Attenuation dB/100ft = 7.98 (from manufacturers' data)
- Velocity factor = 0.66 (from manufacturers' data)
- f(MHz) = 100 (note this is the frequency for which the attenuation figure is quoted)
- Exponent (leave at 0.5 unless you have better data)
Clicking OK to return to the main input screen I now entered the measurement frequency (28.5 MHz), the cable length (26ft), and entered the measured resistance (54 Ohms) and reactance (34 Ohms). Making sure that the "Input Resistance=" option was selected, I hit the Calculate button and got the result Zload = [20.94 + j4.10]. This is close to the expected [22 + j6], but not close enough. I adjusted the cable length entry to 25.8ft and tried again; this time the result was Zload = [21.28 + j6.40]. A final adjustment to 25.85ft gave Zload = [21.19 + j5.82] at which point I decided it was close enough.
I repeated the measurements at 28.0 MHz and 29.0 MHz to check the calibration across the frequency range of interest. Using the 25.85ft value for cable length produced results of [21.40 + j5.94] and [20.99 + j5.65] respectively. These results confirmed that the cable length figure was pretty accurate, and that I could proceed with confidence to measure the antenna feedpoint impedance.
Is all this necessary ? Well, had I not calibrated the cable length nor taken account of the cable losses the predicted load impedance would have been [26.41 + j4.11] - a long way from the real figure of [22 + j6].
Finally, I find that the analyser often gets the sign of the reactive component wrong, so when logging my antenna measurements I ignore it and just note the magnitude of the reactance. Then when I enter the data into the Transmission Line Calculator applet I check the load impedance with positive, and then negative, signs; usually one of the results looks close to the expected antenna impedance, whereas the other looks "silly" and can be ignored. I've yet to find a case where the real sign cannot be resolved unambiguously.